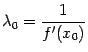 , при
котором все секущие параллельны касательной, проведённой к графику
, при
котором все секущие параллельны касательной, проведённой к графику Заметим, что в методе секущих удобно было бы фиксировать наиболее удобное для
первого шага значение 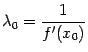 , при
котором все секущие параллельны касательной, проведённой к графику
, при
котором все секущие параллельны касательной, проведённой к графику ![]() при
при ![]() . При таком
выборе
. При таком
выборе ![]() метод
секущих называется методом одной касательной. Формула
итераций этого метода имеет вид
метод
секущих называется методом одной касательной. Формула
итераций этого метода имеет вид

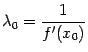 или, что
то же,
или, что
то же, 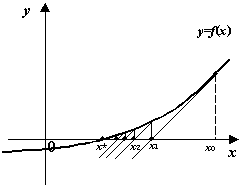
При таком выборе ![]() в точке
в точке
![]() выполнено равенство
выполнено равенство
В качестве начального приближения возьмём ![]() . Поскольку
. Поскольку
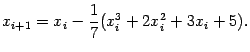
Проверьте, сколько нужно итераций, чтобы найти то же значение корня, начав с ![]() и с
и с ![]() .
.
Ответ: Потребуется и в том, и в другом случае 22 итерации.